ΤΟ ΘΡΥΛΙΚΟ ΕΝΤΕΡΠΑΪΖ ΚΑΙ ΤΟ STAR TREK ΔΙΚΑΙΩΝΟΝΤΑΙ
του Θεόφραστου Ανδρεόπουλου
Την πειραματική επιβεβαίωση της Θεωρίας της Γενικής Σχετικότητας του Α.Άινσταϊν είναι έτοιμοι να αποδείξουν οι επιστήμονες με βάση την οποία υπάρχου τα λεγόμενα βαρυτικά κύματα και καμπυλώνουν τον Χωροχρόνο μέσα στον οποίο ζούμε όλοι μας.
Για πολλούς η καμπύλωση του Χωροχρόνου αποτελεί την μόνη διέξοδο για μελλοντικά αστρικά ταξίδια και "διαδρομές" μέσα στον Χρόνο.
Το μη επανδρωμένο διαστημικό εργαστήριο LISA Pathfinder εκτόξευσε χθες η Ευρωπαϊκή Υπηρεσία Διαστήματος ESA, με στόχο την πειραματική επιβεβαίωση της Θεωρίας της Σχετικότητας του Αϊνστάιν.
"
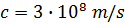 , σε όλα τα αδρανειακά συστήματα αναφοράς.
, σε όλα τα αδρανειακά συστήματα αναφοράς.
Με άλλα λόγια, οποιοσδήποτε μετρά την ταχύτητα του φωτός θα βρει την ίδια τιμή, c. Αν αποδεχθούμε τη Θεωρία της σχετικότητας του Einstein, πρέπει να συμπεράνουμε ότι η σχετική κίνηση δεν έχει καμιά σημασία για τη μέτρηση της ταχύτητας του φωτός.
Αν μελετήσει κανείς ορισμένες από τις συνέπειες της σχετικότητας όπως αναφέρει το άρθρο του christianity-science.gr, θα διαπιστώσει ότι αντιτίθενται στις βασικές ιδέες μας για τον χώρο και τον χρόνο. Θα περιορίσουμε τη μελέτη μας στην έννοια του του χρόνου και του ταυτοχρονισμού, οι οποίες είναι εντελώς διαφορετικές στη σχετικιστική μηχανική από ό,τι είναι στη νευτώνεια μηχανική.
Ομοίως συμβαίνει και για το μήκος (το οποίο όμως δεν αποτελεί αντικείμενο μελέτης του παρόντος άρθρου). Παραδείγματος χάριν μερικές συνέπειες της σχετικότητας είναι ότι η απόσταση μεταξύ δύο σημείων και το χρονικό διάστημα μεταξύ δύο συμβάντων εξαρτώνται από το σύστημα αναφοράς στο οποίο μετρούνται.
Αυτό σημαίνει ότι στη σχετικότητα δεν υπάρχει η έννοια του απόλυτου μήκους ή του απόλυτου χρόνου. Επίπλέον, συμβάντα που συντελούνται ταυτοχρόνως σε διαφορετικές θέσεις σε ένα σύστημα, δεν είναι, εν γένει, ταυτόχρονα σε ένα άλλο σύστημα.
Προκειμένου να επεξηγήσει το σημείο αυτό, ο Einstein επινόησε το εξής νοητικό πείραμα. 'Ενα όχημα κινείται με σταθερή ταχύτητα όταν δύο κεραυνοί χτυπούν τα άκρα του οχήματος, όπως δείχνει το Σχήμα 1α, αφήνοντας σημάδια στο όχημα και στο έδαφος. 'Εστωσαν Α' και Β' τα σημάδια που αποτυπώνονται στο όχημα και Α και Β τα αντίστοιχα σημάδια που αποτυπώνονται στο έδαφος.
Ένας παρατηρητής στο σημείο Ο', ο οποίος κινείται με το όχημα, βρίσκεται στο μέσο της απόστασης μεταξύ των Α' και Β', ενώ ένας ακίνητος παρατηρητής στο σημείο Ο του εδάφους βρίσκεται στο μέσο της απόστασης μεταξύ των Α και Β. Τα συμβάντα που καταγράφονται από τους δύο παρατηρητές είναι τα φωτεινά σήματα που εκπέμπονται από τους κεραυνούς.
Ας υποθέσουμε ότι τα δύο φωτεινά σήματα φθάνουν στον ακίνητο παρατηρητή στο Ο την ίδια χρονική στιγμή, όπως φαίνεται στο Σχήμα 1β. Αυτός ο παρατηρητής αντιλαμβάνεται ότι τα φωτεινά σήματα έχουν διανύσει ίσες αποστάσεις με την ίδια ταχύτητα. Έτσι ο παρατηρητής στο σημείο Ο ορθά συμπεραίνει ότι τα συμβάντα στα σημεία Α και Β συντελούνται ταυτοχρόνως.
Τώρα ας θεωρήσουμε τα ίδια συμβάντα, όπως τα αντιλαμβάνεται ο κινούμενος παρατηρητής στο σημείο Ο' του οχήματος. Τη χρονική στιγμή που τα φωτεινά σήματα φθάνουν στον ακίνητο παρατηρητή στο Ο, ο παρατηρητής στο Ο' έχει μετακινηθεί, όπως φαίνεται στο Σχήμα 1β. Συνεπώς, το φωτεινό σήμα από το Β' έχει ήδη αφιχθεί στο Ο', ενώ το φωτεινό σήμα από το Α' δεν έχει ακόμη φθάσει στο Ο'.
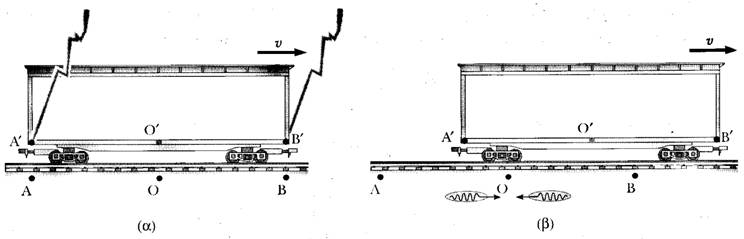
Σχήμα 1: Δύο κεραυνοί χτυπούν τα άκρα ενός κινούμενου οχήματος. (α) Τα συμβάντα φαίνονται ότι είναι ταυτόχρονα
για τον ακίνητο παρατηρητή στο Ο, ο οποίος βρίσκεται στο μέσο της απόστασης μεταξύ των Α και Β. (β) Τα συμβάντα
δεν φαίνονται ότι είναι ταυτόχρονα για τον κινούμενο παρατηρητή στο Ο', ο οποίος υποστηρίζει ότι το πρόσθιο άκρο
του οχήματος υφίσταται το χτύπημα του κεραυνού πριν από το οπίσθιο άκρο
Σύμφωνα με τον Einstein, o παρατηρητής στο O' πρέπει να παρατηρεί ότι το φως διαδίδεται με την ίδια ταχύτητα που μετρείται και από τον παρατηρητή στο O. Συνεπώς, o παρατηρητής στο O' συμπεραίνει ότι o κεραυνός χτυπά το πρόσθιο άκρο του οχήματος προτού χτυπήσει το οπίσθιο άκρο. Αυτό το ιδεατό πείραμα δείχνει σαφώς ότι τα δύο συμβάντα, τα οποία φαίνονται ότι είναι ταυτόχρονα για τον παρατηρητή στο O, δεν φαίνονται να είναι ταυτόχρονα για τον παρατηρητή στο Ο'. Με άλλα λόγια,
δύο συμβάντα τα οποία είναι ταυτόχρονα σε ένα σύστημα αναφοράς, δεν είναι, εν γένει, ταυτόχρονα σε ένα δεύτερο σύστημα που κινείται ως προς το πρώτο. Αυτό σημαίνει ότι o ταυτοχρονισμός δεν είναι απόλυτη έννοια.
Σ’ αυτό το σημείο, ίσως αναρωτηθείτε ποια από τις δύο παρατηρήσεις είναι σωστή σε ό,τι αφορά τα δύο συμβάντα. H απάντηση είναι ότι και οι δύο είναι σωστές, επειδή η Αρχή της Σχετικότητας αναφέρει ότι δεν υπάρχει κάποιο προνομιακό αδρανειακό σύστημα αναφοράς.
Μολονότι οι δύο παρατηρητές καταλήγουν σε διαφορετικά συμπεράσματα, και οι δύο έχουν δίκιο στο δικό τους σύστημα αναφοράς, επειδή η έννοια του ταυτοχρονισμού δεν είναι απόλυτη. Πράγματι, αυτό είναι το κεντρικό σημείο της σχετικότητας – δηλαδή κάθε αδρανειακό σύστημα αναφοράς μπορεί να χρησιμοποιηθεί για την καταγραφή συμβάντων και τη μελέτη φυσικών φαινομένων. Δεν υπάρχει κάτι το λανθασμένο με τα ρολόγια ή με τα υποδεκάμετρα που χρησιμοποιούνται για την πραγματοποίηση των μετρήσεων. Απλώς τα χρονικά διαστήματα και οι μετρήσεις μήκους εξαρτώνται από τον παρατηρητή.
Παρατηρητές σε διαφορετικά αδρανειακά συστήματα αναφοράς θα μετρούν διαφορετικά χρονικά διαστήματα με τα ρολόγια τους και διαφορετικές αποστάσεις με τα υποδεκάμετρά τους. Ωστόσο, και οι δύο Θα συμφωνούν σε ό,τι αφορά τους νόμους της φυσικής στα αντίστοιχα συστήματα αναφοράς τους, αφού οι νόμοι αυτοί είναι οι ίδιοι για όλους τους αδρανειακούς παρατηρητές.
H σχετικότητα που διέπει τις μετρήσεις χρόνου και αποστάσεων δίνει τη δυνατότητα στους νόμους της φυσικής (συμπεριλαμβανομένων και των εξισώσεων του Maxwell) να είναι ίδιοι για όλους τους παρατηρητές που κινούνται με σταθερή ταχύτητα.
Διαστολή χρόνου
Προκειμένου να δείξουμε ότι o χρόνος δεν ρέει με τον ίδιο ρυθμό για δύο διαφορετικούς αδρανειακούς παρατηρητές, ας θεωρήσουμε ένα όχημα κινούμενο προς τα δεξιά με ταχύτητα u, όπως δείχνει το Σχήμα 2α. Στην οροφή του οχήματος είναι στερεωμένο ένα κάτοπτρο· και ένας παρατηρητής στο Ο', που βρίσκεται σε ακινησία ως προς το όχημα, κρατάει μια λυχνία φωτεινών παλμών σε απόσταση d από το κάτοπτρο. Σε κάποια στιγμή, η λυχνία εκπέμπει έναν φωτεινό παλμό. Επειδή o φωτεινός παλμός έχει ταχύτητα c, o χρόνος που απαιτείται ώστε o παλμός να μεταβεί από τη λυχνία στο κάτοπτρο και να επιστρέψει στη λυχνία μπορεί να βρεθεί από τον ορισμό της ταχύτητας:
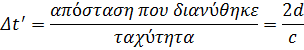
όπου η τονούμενη σημειογραφία δηλώνει ότι o χρόνος μετρήθηκε από τον παρατηρητή στο σύστημα αναφοράς του κινούμενου οχήματος.
Τώρα, ας εξετάσουμε το ίδιο σύνολο συμβάντων, όπως παρατηρούνται από έναν παρατηρητή που βρίσκεται στο σημείο O ενός ακίνητου συστήματος αναφοράς (Σχ. 2β). Σύμφωνα με τον παρατηρητή αυτόν, το κάτοπτρο και η λυχνία κινούνται προς τα δεξιά με ταχύτητα u. Τη στιγμή που το φως από τη λυχνία φθάνει στο κάτοπτρο, το κάτοπτρο θα έχει διανύσει μία απόσταση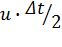 ,
όπου Δt είναι ο χρόνος που απαιτείται ώστε ο φωτεινός παλμός να μεταβεί
από τη λυχνία στο κάτοπτρο και να επιστρέψει στη λυχνία, όπως μετρείται
από τον ακίνητο παρατηρητή που βρίσκεται στο Ο. Με άλλα λόγια, λόγω της
κίνησης του συστήματος, ο ακίνητος παρατηρητής συμπεραίνει ότι,
προκειμένου ο παλμός να προσπέσει στο κάτοπτρο πρέπει να φύγει από τη
λυχνία υπό γωνία ως προς την κατακόρυφη διεύθυνση. Συγκρίνοντας τα
Σχήματα 2α και 2β, βλέπουμε ότι το φως πρέπει να διανύσει μεγαλύτερη
απόσταση στο ακίνητο σύστημα από ό,τι στο κινούμενο σύστημα.
,
όπου Δt είναι ο χρόνος που απαιτείται ώστε ο φωτεινός παλμός να μεταβεί
από τη λυχνία στο κάτοπτρο και να επιστρέψει στη λυχνία, όπως μετρείται
από τον ακίνητο παρατηρητή που βρίσκεται στο Ο. Με άλλα λόγια, λόγω της
κίνησης του συστήματος, ο ακίνητος παρατηρητής συμπεραίνει ότι,
προκειμένου ο παλμός να προσπέσει στο κάτοπτρο πρέπει να φύγει από τη
λυχνία υπό γωνία ως προς την κατακόρυφη διεύθυνση. Συγκρίνοντας τα
Σχήματα 2α και 2β, βλέπουμε ότι το φως πρέπει να διανύσει μεγαλύτερη
απόσταση στο ακίνητο σύστημα από ό,τι στο κινούμενο σύστημα.
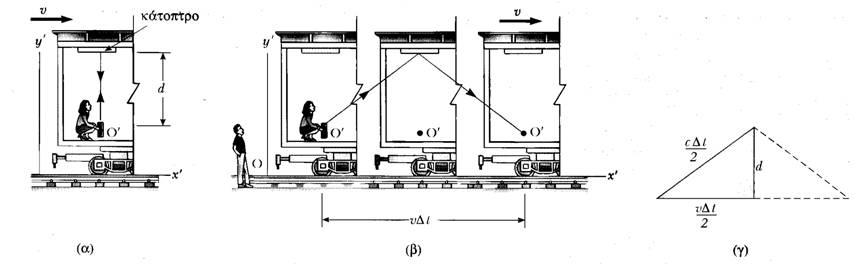
Σχήμα 2: (α) Ένα κάτοπτρο είναι στερεωμένο σε ένα κινούμενο όχημα και ένας φωτεινός παλμός εκπέμπεται από το σημείο Ο', το οποίο βρίσκεται
σε ηρεμία ως προς το όχημα. (β) Σε σχέση με τον ακίνητο παρατηρητή στο έδαφος, το κάτοπτρο και η πηγή παλμών Ο' κινούνται με ταχύτητα u.
Σημειώστε ότι η απόσταση που διανύει ο παλμός όπως αυτή μετρείται από τον ακίνητο παρατηρητή είναι μεγαλύτερη από 2d. (γ) Το ορθογώνιο
τρίγωνο για τον υπολογισμό της σχέσης μεταξύ Δt και Δt'
Τώρα, σύμφωνα με τον Einstein, η ταχύτητα του φωτός πρέπει να είναι c και για τους δύο παρατηρητές. Συνεπώς, προκύπτει ότι το χρονικό διάστημα Δt που μετρείται από έναν παρατηρητή στο ακίνητο σύστημα είναι μεγαλύτερο από το χρονικό διάστημα Δt' που μετρείται από έναν παρατηρητή στο κινούμενο σύστημα. Για να βρούμε τη σχέση μεταξύ των Δt και Δt', είναι βολικό να χρησιμοποιήσουμε το ορθογώνιο τρίγωνο του Σχήματος 2γ. Η εφαρμογή του πυθαγόρειου Θεωρήματος στο συγκεκριμένο τρίγωνο δίνει
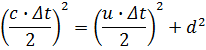
Λύνοντας ως προς Δt έχουμε:
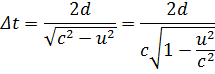
Επειδή είναι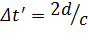 , μπορούμε να γράψουμε την προηγούμενη εξίσωση ως εξής
, μπορούμε να γράψουμε την προηγούμενη εξίσωση ως εξής
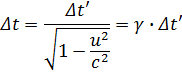
όπου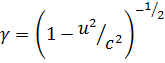 .
Το αποτέλεσμα αυτό δηλώνει ότι το χρονικό διάστημα που μετρείται από
τον παρατηρητή στο ακίνητο σύστημα είναι μεγαλύτερο από εκείνο που
μετρείται από τον παρατηρητή στο κινούμενο σύστημα (επειδή το γ είναι
πάντοτε μεγαλύτερο από τη μονάδα).
.
Το αποτέλεσμα αυτό δηλώνει ότι το χρονικό διάστημα που μετρείται από
τον παρατηρητή στο ακίνητο σύστημα είναι μεγαλύτερο από εκείνο που
μετρείται από τον παρατηρητή στο κινούμενο σύστημα (επειδή το γ είναι
πάντοτε μεγαλύτερο από τη μονάδα).
Σύμφωνα με έναν ακίνητο παρατηρητή, ένα κινούμενο ρολόι είναι
πιο αργό κατά έναν συντελεστή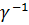 από ένα ολόιδιο ακίνητο ρολόι.
από ένα ολόιδιο ακίνητο ρολόι.
Το φαινόμενο αυτό είναι γνωστό ως διαστολή του χρόνου.
Το χρονικό διάστημα Δt' ονομάζεται ιδιοχρόνος. Γενικά, ιδιοχρόνος ορίζεται το χρονικό διάστημα που μεσολαβεί μεταξύ δύο συμβάντων όταν η μέτρηση γίνεται από έναν παρατηρητή που βλέπει τα γεγονότα να συμβαίνουν στην ίδια θέση. Στην περίπτωσή μας, ο παρατηρητής στο Ο' μετράει τον ιδιοχρόνο. δηλαδή, ιδιοχρόνος είναι πάντοτε, ο χρόνος που μετρείται από έναν παρατηρητή ο οποίος κινείται μαζί με το ρολόι.
Είδαμε ότι τα κινούμενα ρολόγια «πάνε πιο αργά» κατά τον συντελεστή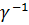 .
Αυτό ισχύει και για τα συνήθη μηχανικά ρολόγια, καθώς και για το ρολόι
«φωτός» που μόλις περιγράφηκε. Πράγματι, μπορούμε να γενικεύσουμε αυτά
τα αποτελέσματα αναφέροντας ότι όλες οι φυσικές διεργασίες,
συμπεριλαμβανομένων των χημικών αντιδράσεων και των βιολογικών
διεργασιών, επιβραδύνονται σε, σχέση με ένα ακίνητο ρολόι όταν
συμβαίνουν σε ένα κινούμενο σύστημα.
.
Αυτό ισχύει και για τα συνήθη μηχανικά ρολόγια, καθώς και για το ρολόι
«φωτός» που μόλις περιγράφηκε. Πράγματι, μπορούμε να γενικεύσουμε αυτά
τα αποτελέσματα αναφέροντας ότι όλες οι φυσικές διεργασίες,
συμπεριλαμβανομένων των χημικών αντιδράσεων και των βιολογικών
διεργασιών, επιβραδύνονται σε, σχέση με ένα ακίνητο ρολόι όταν
συμβαίνουν σε ένα κινούμενο σύστημα.
Παραδείγματος χάριν, ο σφυγμός ενός αστροναύτη που κινείται στο Διάστημα θα πρέπει να προσαρμοστεί με την κλίμακα χρόνου ενός ρολογιού που βρίσκεται μέσα στο διαστημόπλοιο. Το ρολόι του αστροναύτη και ο σφυγμός του επιβραδύνονται σε σχέση με ένα ακίνητο ρολόι. Ο αστροναύτης όμως, προφανώς δεν αντιλαμβάνεται ότι ο ρυθμός ζωής επιβραδύνεται στο διαστημόπλοιο.
Η διαστολή του χρόνου είναι ένα πραγματικό φαινόμενο που έχει επιβεβαιωθεί με διάφορα πειράματα.
Αποσπάσματα από το βιβλίο: «Σύγχρονη Φυσική» - Κεφάλαιο 1ο των R.A.Serway – C.J.Moses – C.A.Moyer,
Πανεπιστημιακές Εκδόσεις Κρήτης 2001
Η σκέψη είναι απλή, "δεν πάμε στο βουνό εμείς, φέρνουμε το βουνό σε εμάς", είναι η αντίστροφη πορεία του "αίτιου και αιτιατού" και αυτό από μόνο του, αρκεί για να αλλάξει τον τρόπο που σκέφτεται η Ανθρωπότητα.
Πηγή
του Θεόφραστου Ανδρεόπουλου
Την πειραματική επιβεβαίωση της Θεωρίας της Γενικής Σχετικότητας του Α.Άινσταϊν είναι έτοιμοι να αποδείξουν οι επιστήμονες με βάση την οποία υπάρχου τα λεγόμενα βαρυτικά κύματα και καμπυλώνουν τον Χωροχρόνο μέσα στον οποίο ζούμε όλοι μας.
Για πολλούς η καμπύλωση του Χωροχρόνου αποτελεί την μόνη διέξοδο για μελλοντικά αστρικά ταξίδια και "διαδρομές" μέσα στον Χρόνο.
Το μη επανδρωμένο διαστημικό εργαστήριο LISA Pathfinder εκτόξευσε χθες η Ευρωπαϊκή Υπηρεσία Διαστήματος ESA, με στόχο την πειραματική επιβεβαίωση της Θεωρίας της Σχετικότητας του Αϊνστάιν.
Ο πύραυλος Βέγκα, που εκτοξεύθηκε χθες με επιτυχία από τη
διαστημική βάση του Κουρού στη Γαλλική Γουιάνα, μετέφερε το εργαστήριο
σε τροχιά, με σκοπό την παρατήρηση βαρυτικών κυμάτων στο διάστημα.
"
Την ύπαρξη βαρυτικών κυμάτων είχε προβλέψει ο Αϊνστάιν στη Γενική
Θεωρία της Σχετικότητας, που δημοσιεύθηκε στις 2 Δεκεμβρίου 1915.
Η θεωρία του θέλει τα κύματα αυτά να εμφανίζονται σε κάθε σημείο
του σύμπαντος και να προκαλούνται από γιγάντια επιταχυνόμενα
αντικείμενα. Μέχρι στιγμής, τα βαρυτικά κύματα δεν έχουν εντοπισθεί,
εξαιτίας της πολύ μικρής τους ισχύος.
«Τα κύματα που εκπέμπονται από δύο μαύρες τρύπες σε τροχιά η μία
γύρω από την άλλη θα μετακινούσαν χάρακα μήκους ενός εκατομμυρίου
χιλιομέτρων, κατά ένα και μόνον άτομο», αναφέρει στην ανακοίνωσή της η
ESA.
Το κρίσιμο πείραμα του LISA Pathfinder θα πραγματοποιηθεί χάρη σε
δύο μικρούς ομοιόμορφους επίχρυσους κύβους από πλατίνα, σε απόσταση 38
εκατοστών ο ένας από τον άλλο. Απομονωμένοι από κάθε εξωτερική και
εσωτερική δύναμη, εκτός από τη βαρύτητα, οι κύβοι θα βρεθούν σε ελεύθερη
πτώση, ώστε να διαπιστωθεί εάν η θέση τους θα μεταβληθεί λόγω των
βαρυτικών κυμάτων.
Η γενική σχετικότητα είναι μια θεωρία βαρύτητας που αναπτύχθηκε από τον Άινσταϊν την περίοδο 1907-2015
Η ανάπτυξη της γενικής σχετικότητας ξεκίνησε με την αρχή της ισοδυναμίας, σύμφωνα με την οποία οι καταστάσεις επιταχυνόμενης κίνησης και ηρεμίας σε ένα βαρυτικό πεδίο (για παράδειγμα πάνω στην επιφάνεια της Γης) είναι ταυτόσημες.
Το αποτέλεσμα της ιδέας αυτής είναι ότι η ελεύθερη πτώση είναι αδρανειακή κίνηση σε μη ευκλείδειο χώρο: Με άλλα λόγια, ένα αντικείμενο σε ελεύθερη πτώση, πέφτει επειδή αυτός είναι ο τρόπος με τον οποίο τα αντικείμενα κινούνται όταν δεν ασκείται πάνω τους δύναμη, αντί να πέφτει λόγω της δύναμης της βαρύτητας, όπως συμβαίνει στην κλασική μηχανική.
Αυτό είναι ασύμβατο με την κλασική μηχανική και την ειδική σχετικότητα, επειδή σε αυτές τις θεωρίες αντικείμενα που κινούνται αδρανειακά δε μπορούν να επιταχύνουν το ένα σε σχέση με το άλλο, αλλά αντικείμενα σε ελεύθερη πτώση κάνουν ακριβώς αυτό.
Για να λυθεί η δυσκολία, ο Άινσταϊν πρότεινε αρχικά πως ο χωροχρόνος είναι καμπυλωμένος. Το 1915 ανακοίνωσε τις πεδιακές εξισώσεις Άινσταϊν, οι οποίες συσχετίζουν την καμπύλωση του χωροχρόνου σε σχέση με τη μάζα, την ενέργεια και την ορμή μέσα σε αυτόν.
Σύμφωνα με τη γενική θεωρία της σχετικότητας:
Το αποτέλεσμα της ιδέας αυτής είναι ότι η ελεύθερη πτώση είναι αδρανειακή κίνηση σε μη ευκλείδειο χώρο: Με άλλα λόγια, ένα αντικείμενο σε ελεύθερη πτώση, πέφτει επειδή αυτός είναι ο τρόπος με τον οποίο τα αντικείμενα κινούνται όταν δεν ασκείται πάνω τους δύναμη, αντί να πέφτει λόγω της δύναμης της βαρύτητας, όπως συμβαίνει στην κλασική μηχανική.
Αυτό είναι ασύμβατο με την κλασική μηχανική και την ειδική σχετικότητα, επειδή σε αυτές τις θεωρίες αντικείμενα που κινούνται αδρανειακά δε μπορούν να επιταχύνουν το ένα σε σχέση με το άλλο, αλλά αντικείμενα σε ελεύθερη πτώση κάνουν ακριβώς αυτό.
Για να λυθεί η δυσκολία, ο Άινσταϊν πρότεινε αρχικά πως ο χωροχρόνος είναι καμπυλωμένος. Το 1915 ανακοίνωσε τις πεδιακές εξισώσεις Άινσταϊν, οι οποίες συσχετίζουν την καμπύλωση του χωροχρόνου σε σχέση με τη μάζα, την ενέργεια και την ορμή μέσα σε αυτόν.
Σύμφωνα με τη γενική θεωρία της σχετικότητας:
- Ο χρόνος περνά διαφορετικά σε χαμηλότερα βαρυτικά δυναμικά. Το φαινόμενο αυτό ονομάζεται βαρυτική διαστολή του χρόνου.
- Οι τροχιές μεταβάλλονται με τρόπο μη αναμενόμενο από τη θεωρία του Νεύτωνα για τη βαρύτητα.
- Ακόμα και οι ακτίνες του φωτός (όπου τα φωτόνια δεν έχουν μάζα) αλλάζουν πορεία παρουσία ενός βαρυτικού πεδίου.
- Ερμηνεύει τη διαστολή του Σύμπαντος, και τα μακρινά μέρη του απομακρύνονται από εμάς σχεδόν με την ταχύτητα του φωτός. Αυτό δεν αντιτίθεται στην ειδική σχετικότητα, καθώς είναι το ίδιο το Σύμπαν το οποίο διαστέλλεται.
Η ειδική σχετικότητα είναι μια θεωρία για τη δομή του χωροχρόνου, την οποία εισήγαγε ο Άλμπερτ Άινσταϊν το 1905. Βασίζεται σε δύο αξιώματα τα οποία είναι αντίθετα με την κλασική μηχανική:
Η ειδική θεωρία της σχετικότητας εισάγει επίσης τις έννοιες της μάζας ηρεμίας και της μάζας αδρανείας για κάθε παρατηρούμενο σώμα. Ο διαχωρισμός αυτός οφείλεται στο ότι η παρατηρούμενη μάζα ενός σώματος εξαρτάται από την ταχύτητά του σε σχέση με τον παρατηρητή.
Μάζα ηρεμίας είναι η μάζα του σώματος όταν αυτό είναι ακίνητο σε σχέση με κάποιον παρατηρητή και μάζα αδρανείας η παρατηρούμενη μάζα όταν το σώμα κινείται. Όσο μεγαλύτερη είναι η παρατηρούμενη ταχύτητα ένος σώματος τόσο μεγαλύτερη είναι και η παρατηρούμενη μάζα του. Είναι αδύνατο ένα σώμα να έχει μάζα και να κινείται με την ταχύτητα του φωτός καθώς σε αντίθετη περίπτωση η μάζα αδρανείας του θα πρέπει να είναι άπειρη, ανεξαρτήτως του μεγέθους της μάζας ηρεμίας.
Η ταχύτητα του φωτός στο κενό έχει την ίδια τιμή,- Οι νόμοι της φυσικής είναι οι ίδιοι για όλους τους παρατηρητές που βρίσκονται σε αδρανειακό σύστημα αναφοράς (αρχή σχετικότητας του Γαλιλαίου).
- Η ταχύτητα του φωτός στο κενό είναι ίδια για όλους τους παρατηρητές, ανεξαρτήτως της σχετικής τους κίνησης ή της κίνησης της πηγής του φωτός.
- Διαστολή χρόνου: Τα ρολόγια δύο παρατηρητών που κινούνται με διαφορετική ταχύτητα, γυρνάνε με διαφορετικό ρυθμό. Για τον ταχύτερο παρατηρητή το ρολόι γυρνάει πιο αργά. Από αυτήν την αρχή προκύπτει το παράδοξο των διδύμων).
- Συστολή του μήκους: Τα μήκη που μετρούν δύο παρατηρητές που κινούνται με διαφορετική ταχύτητα είναι διαφορετικά. Για τον ταχύτερο παρατηρητή τα μήκη είναι μικρότερα.
- Σχετικότητα της ταυτοχρονικότητας: Δύο γεγονότα που φαίνονται να συμβαίνουν ταυτόχρονα σε έναν παρατηρητή Α, δε θα συμβαίνουν ταυτόχρονα για έναν παρατηρητή Β, εάν ο Β κινείται σε σχέση με τον Α.
- Ισοδυναμία μάζας-ενέργειας: Από τη σχέση E = mc², η ενέργεια και η μάζα είναι ισοδύναμες.
Η ειδική θεωρία της σχετικότητας εισάγει επίσης τις έννοιες της μάζας ηρεμίας και της μάζας αδρανείας για κάθε παρατηρούμενο σώμα. Ο διαχωρισμός αυτός οφείλεται στο ότι η παρατηρούμενη μάζα ενός σώματος εξαρτάται από την ταχύτητά του σε σχέση με τον παρατηρητή.
Μάζα ηρεμίας είναι η μάζα του σώματος όταν αυτό είναι ακίνητο σε σχέση με κάποιον παρατηρητή και μάζα αδρανείας η παρατηρούμενη μάζα όταν το σώμα κινείται. Όσο μεγαλύτερη είναι η παρατηρούμενη ταχύτητα ένος σώματος τόσο μεγαλύτερη είναι και η παρατηρούμενη μάζα του. Είναι αδύνατο ένα σώμα να έχει μάζα και να κινείται με την ταχύτητα του φωτός καθώς σε αντίθετη περίπτωση η μάζα αδρανείας του θα πρέπει να είναι άπειρη, ανεξαρτήτως του μεγέθους της μάζας ηρεμίας.
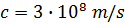 , σε όλα τα αδρανειακά συστήματα αναφοράς.
, σε όλα τα αδρανειακά συστήματα αναφοράς.Με άλλα λόγια, οποιοσδήποτε μετρά την ταχύτητα του φωτός θα βρει την ίδια τιμή, c. Αν αποδεχθούμε τη Θεωρία της σχετικότητας του Einstein, πρέπει να συμπεράνουμε ότι η σχετική κίνηση δεν έχει καμιά σημασία για τη μέτρηση της ταχύτητας του φωτός.
Αν μελετήσει κανείς ορισμένες από τις συνέπειες της σχετικότητας όπως αναφέρει το άρθρο του christianity-science.gr, θα διαπιστώσει ότι αντιτίθενται στις βασικές ιδέες μας για τον χώρο και τον χρόνο. Θα περιορίσουμε τη μελέτη μας στην έννοια του του χρόνου και του ταυτοχρονισμού, οι οποίες είναι εντελώς διαφορετικές στη σχετικιστική μηχανική από ό,τι είναι στη νευτώνεια μηχανική.
Ομοίως συμβαίνει και για το μήκος (το οποίο όμως δεν αποτελεί αντικείμενο μελέτης του παρόντος άρθρου). Παραδείγματος χάριν μερικές συνέπειες της σχετικότητας είναι ότι η απόσταση μεταξύ δύο σημείων και το χρονικό διάστημα μεταξύ δύο συμβάντων εξαρτώνται από το σύστημα αναφοράς στο οποίο μετρούνται.
Αυτό σημαίνει ότι στη σχετικότητα δεν υπάρχει η έννοια του απόλυτου μήκους ή του απόλυτου χρόνου. Επίπλέον, συμβάντα που συντελούνται ταυτοχρόνως σε διαφορετικές θέσεις σε ένα σύστημα, δεν είναι, εν γένει, ταυτόχρονα σε ένα άλλο σύστημα.
Μια βασική παραδοχή της νευτώνειας μηχανικής είναι ότι υπάρχει μια παγκόσμια κλiμακα χρόνου η οποία είναι ίδια για όλους τους παρατηρητές. Πράγματι, ο Νεύτων έγραφε ότι «Ο απόλυτος, αληθινός και μαθηματικός χρόνος, από την ίδια του τη φύση, ρέει ομοιόμορφα χωρίς καμιά συσχέτιση με οτιδήποτε το εξωτερικό».
Έτσι, ο Νεύτων και οι υποστηρικτές του θεώρησαν το ταυτόχρονο, απλώς, ως δεδομένο. Στην ειδική θεωρία της σχετικότητας, ο Einstein εγκατέλειψε αυτήν την υπόθεση. Σύμφωνα με τον Einstein, οι μετρήσεις, χρονικών διαστημάτων εξαρτώνται από το σύστημα αναφοράς στο οποίο γίνεται η μέτρηση.Προκειμένου να επεξηγήσει το σημείο αυτό, ο Einstein επινόησε το εξής νοητικό πείραμα. 'Ενα όχημα κινείται με σταθερή ταχύτητα όταν δύο κεραυνοί χτυπούν τα άκρα του οχήματος, όπως δείχνει το Σχήμα 1α, αφήνοντας σημάδια στο όχημα και στο έδαφος. 'Εστωσαν Α' και Β' τα σημάδια που αποτυπώνονται στο όχημα και Α και Β τα αντίστοιχα σημάδια που αποτυπώνονται στο έδαφος.
Ένας παρατηρητής στο σημείο Ο', ο οποίος κινείται με το όχημα, βρίσκεται στο μέσο της απόστασης μεταξύ των Α' και Β', ενώ ένας ακίνητος παρατηρητής στο σημείο Ο του εδάφους βρίσκεται στο μέσο της απόστασης μεταξύ των Α και Β. Τα συμβάντα που καταγράφονται από τους δύο παρατηρητές είναι τα φωτεινά σήματα που εκπέμπονται από τους κεραυνούς.
Ας υποθέσουμε ότι τα δύο φωτεινά σήματα φθάνουν στον ακίνητο παρατηρητή στο Ο την ίδια χρονική στιγμή, όπως φαίνεται στο Σχήμα 1β. Αυτός ο παρατηρητής αντιλαμβάνεται ότι τα φωτεινά σήματα έχουν διανύσει ίσες αποστάσεις με την ίδια ταχύτητα. Έτσι ο παρατηρητής στο σημείο Ο ορθά συμπεραίνει ότι τα συμβάντα στα σημεία Α και Β συντελούνται ταυτοχρόνως.
Τώρα ας θεωρήσουμε τα ίδια συμβάντα, όπως τα αντιλαμβάνεται ο κινούμενος παρατηρητής στο σημείο Ο' του οχήματος. Τη χρονική στιγμή που τα φωτεινά σήματα φθάνουν στον ακίνητο παρατηρητή στο Ο, ο παρατηρητής στο Ο' έχει μετακινηθεί, όπως φαίνεται στο Σχήμα 1β. Συνεπώς, το φωτεινό σήμα από το Β' έχει ήδη αφιχθεί στο Ο', ενώ το φωτεινό σήμα από το Α' δεν έχει ακόμη φθάσει στο Ο'.

Σχήμα 1: Δύο κεραυνοί χτυπούν τα άκρα ενός κινούμενου οχήματος. (α) Τα συμβάντα φαίνονται ότι είναι ταυτόχρονα
για τον ακίνητο παρατηρητή στο Ο, ο οποίος βρίσκεται στο μέσο της απόστασης μεταξύ των Α και Β. (β) Τα συμβάντα
δεν φαίνονται ότι είναι ταυτόχρονα για τον κινούμενο παρατηρητή στο Ο', ο οποίος υποστηρίζει ότι το πρόσθιο άκρο
του οχήματος υφίσταται το χτύπημα του κεραυνού πριν από το οπίσθιο άκρο
Σύμφωνα με τον Einstein, o παρατηρητής στο O' πρέπει να παρατηρεί ότι το φως διαδίδεται με την ίδια ταχύτητα που μετρείται και από τον παρατηρητή στο O. Συνεπώς, o παρατηρητής στο O' συμπεραίνει ότι o κεραυνός χτυπά το πρόσθιο άκρο του οχήματος προτού χτυπήσει το οπίσθιο άκρο. Αυτό το ιδεατό πείραμα δείχνει σαφώς ότι τα δύο συμβάντα, τα οποία φαίνονται ότι είναι ταυτόχρονα για τον παρατηρητή στο O, δεν φαίνονται να είναι ταυτόχρονα για τον παρατηρητή στο Ο'. Με άλλα λόγια,
δύο συμβάντα τα οποία είναι ταυτόχρονα σε ένα σύστημα αναφοράς, δεν είναι, εν γένει, ταυτόχρονα σε ένα δεύτερο σύστημα που κινείται ως προς το πρώτο. Αυτό σημαίνει ότι o ταυτοχρονισμός δεν είναι απόλυτη έννοια.
Σ’ αυτό το σημείο, ίσως αναρωτηθείτε ποια από τις δύο παρατηρήσεις είναι σωστή σε ό,τι αφορά τα δύο συμβάντα. H απάντηση είναι ότι και οι δύο είναι σωστές, επειδή η Αρχή της Σχετικότητας αναφέρει ότι δεν υπάρχει κάποιο προνομιακό αδρανειακό σύστημα αναφοράς.
Μολονότι οι δύο παρατηρητές καταλήγουν σε διαφορετικά συμπεράσματα, και οι δύο έχουν δίκιο στο δικό τους σύστημα αναφοράς, επειδή η έννοια του ταυτοχρονισμού δεν είναι απόλυτη. Πράγματι, αυτό είναι το κεντρικό σημείο της σχετικότητας – δηλαδή κάθε αδρανειακό σύστημα αναφοράς μπορεί να χρησιμοποιηθεί για την καταγραφή συμβάντων και τη μελέτη φυσικών φαινομένων. Δεν υπάρχει κάτι το λανθασμένο με τα ρολόγια ή με τα υποδεκάμετρα που χρησιμοποιούνται για την πραγματοποίηση των μετρήσεων. Απλώς τα χρονικά διαστήματα και οι μετρήσεις μήκους εξαρτώνται από τον παρατηρητή.
Παρατηρητές σε διαφορετικά αδρανειακά συστήματα αναφοράς θα μετρούν διαφορετικά χρονικά διαστήματα με τα ρολόγια τους και διαφορετικές αποστάσεις με τα υποδεκάμετρά τους. Ωστόσο, και οι δύο Θα συμφωνούν σε ό,τι αφορά τους νόμους της φυσικής στα αντίστοιχα συστήματα αναφοράς τους, αφού οι νόμοι αυτοί είναι οι ίδιοι για όλους τους αδρανειακούς παρατηρητές.
H σχετικότητα που διέπει τις μετρήσεις χρόνου και αποστάσεων δίνει τη δυνατότητα στους νόμους της φυσικής (συμπεριλαμβανομένων και των εξισώσεων του Maxwell) να είναι ίδιοι για όλους τους παρατηρητές που κινούνται με σταθερή ταχύτητα.
Διαστολή χρόνου
Προκειμένου να δείξουμε ότι o χρόνος δεν ρέει με τον ίδιο ρυθμό για δύο διαφορετικούς αδρανειακούς παρατηρητές, ας θεωρήσουμε ένα όχημα κινούμενο προς τα δεξιά με ταχύτητα u, όπως δείχνει το Σχήμα 2α. Στην οροφή του οχήματος είναι στερεωμένο ένα κάτοπτρο· και ένας παρατηρητής στο Ο', που βρίσκεται σε ακινησία ως προς το όχημα, κρατάει μια λυχνία φωτεινών παλμών σε απόσταση d από το κάτοπτρο. Σε κάποια στιγμή, η λυχνία εκπέμπει έναν φωτεινό παλμό. Επειδή o φωτεινός παλμός έχει ταχύτητα c, o χρόνος που απαιτείται ώστε o παλμός να μεταβεί από τη λυχνία στο κάτοπτρο και να επιστρέψει στη λυχνία μπορεί να βρεθεί από τον ορισμό της ταχύτητας:
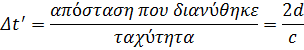
όπου η τονούμενη σημειογραφία δηλώνει ότι o χρόνος μετρήθηκε από τον παρατηρητή στο σύστημα αναφοράς του κινούμενου οχήματος.
Τώρα, ας εξετάσουμε το ίδιο σύνολο συμβάντων, όπως παρατηρούνται από έναν παρατηρητή που βρίσκεται στο σημείο O ενός ακίνητου συστήματος αναφοράς (Σχ. 2β). Σύμφωνα με τον παρατηρητή αυτόν, το κάτοπτρο και η λυχνία κινούνται προς τα δεξιά με ταχύτητα u. Τη στιγμή που το φως από τη λυχνία φθάνει στο κάτοπτρο, το κάτοπτρο θα έχει διανύσει μία απόσταση
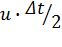 ,
όπου Δt είναι ο χρόνος που απαιτείται ώστε ο φωτεινός παλμός να μεταβεί
από τη λυχνία στο κάτοπτρο και να επιστρέψει στη λυχνία, όπως μετρείται
από τον ακίνητο παρατηρητή που βρίσκεται στο Ο. Με άλλα λόγια, λόγω της
κίνησης του συστήματος, ο ακίνητος παρατηρητής συμπεραίνει ότι,
προκειμένου ο παλμός να προσπέσει στο κάτοπτρο πρέπει να φύγει από τη
λυχνία υπό γωνία ως προς την κατακόρυφη διεύθυνση. Συγκρίνοντας τα
Σχήματα 2α και 2β, βλέπουμε ότι το φως πρέπει να διανύσει μεγαλύτερη
απόσταση στο ακίνητο σύστημα από ό,τι στο κινούμενο σύστημα.
,
όπου Δt είναι ο χρόνος που απαιτείται ώστε ο φωτεινός παλμός να μεταβεί
από τη λυχνία στο κάτοπτρο και να επιστρέψει στη λυχνία, όπως μετρείται
από τον ακίνητο παρατηρητή που βρίσκεται στο Ο. Με άλλα λόγια, λόγω της
κίνησης του συστήματος, ο ακίνητος παρατηρητής συμπεραίνει ότι,
προκειμένου ο παλμός να προσπέσει στο κάτοπτρο πρέπει να φύγει από τη
λυχνία υπό γωνία ως προς την κατακόρυφη διεύθυνση. Συγκρίνοντας τα
Σχήματα 2α και 2β, βλέπουμε ότι το φως πρέπει να διανύσει μεγαλύτερη
απόσταση στο ακίνητο σύστημα από ό,τι στο κινούμενο σύστημα.
Σχήμα 2: (α) Ένα κάτοπτρο είναι στερεωμένο σε ένα κινούμενο όχημα και ένας φωτεινός παλμός εκπέμπεται από το σημείο Ο', το οποίο βρίσκεται
σε ηρεμία ως προς το όχημα. (β) Σε σχέση με τον ακίνητο παρατηρητή στο έδαφος, το κάτοπτρο και η πηγή παλμών Ο' κινούνται με ταχύτητα u.
Σημειώστε ότι η απόσταση που διανύει ο παλμός όπως αυτή μετρείται από τον ακίνητο παρατηρητή είναι μεγαλύτερη από 2d. (γ) Το ορθογώνιο
τρίγωνο για τον υπολογισμό της σχέσης μεταξύ Δt και Δt'
Τώρα, σύμφωνα με τον Einstein, η ταχύτητα του φωτός πρέπει να είναι c και για τους δύο παρατηρητές. Συνεπώς, προκύπτει ότι το χρονικό διάστημα Δt που μετρείται από έναν παρατηρητή στο ακίνητο σύστημα είναι μεγαλύτερο από το χρονικό διάστημα Δt' που μετρείται από έναν παρατηρητή στο κινούμενο σύστημα. Για να βρούμε τη σχέση μεταξύ των Δt και Δt', είναι βολικό να χρησιμοποιήσουμε το ορθογώνιο τρίγωνο του Σχήματος 2γ. Η εφαρμογή του πυθαγόρειου Θεωρήματος στο συγκεκριμένο τρίγωνο δίνει
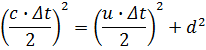
Λύνοντας ως προς Δt έχουμε:
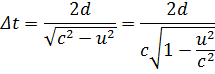
Επειδή είναι
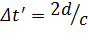 , μπορούμε να γράψουμε την προηγούμενη εξίσωση ως εξής
, μπορούμε να γράψουμε την προηγούμενη εξίσωση ως εξής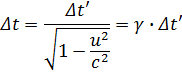
όπου
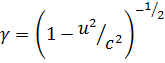 .
Το αποτέλεσμα αυτό δηλώνει ότι το χρονικό διάστημα που μετρείται από
τον παρατηρητή στο ακίνητο σύστημα είναι μεγαλύτερο από εκείνο που
μετρείται από τον παρατηρητή στο κινούμενο σύστημα (επειδή το γ είναι
πάντοτε μεγαλύτερο από τη μονάδα).
.
Το αποτέλεσμα αυτό δηλώνει ότι το χρονικό διάστημα που μετρείται από
τον παρατηρητή στο ακίνητο σύστημα είναι μεγαλύτερο από εκείνο που
μετρείται από τον παρατηρητή στο κινούμενο σύστημα (επειδή το γ είναι
πάντοτε μεγαλύτερο από τη μονάδα).Σύμφωνα με έναν ακίνητο παρατηρητή, ένα κινούμενο ρολόι είναι
πιο αργό κατά έναν συντελεστή
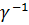 από ένα ολόιδιο ακίνητο ρολόι.
από ένα ολόιδιο ακίνητο ρολόι.Το φαινόμενο αυτό είναι γνωστό ως διαστολή του χρόνου.
Το χρονικό διάστημα Δt' ονομάζεται ιδιοχρόνος. Γενικά, ιδιοχρόνος ορίζεται το χρονικό διάστημα που μεσολαβεί μεταξύ δύο συμβάντων όταν η μέτρηση γίνεται από έναν παρατηρητή που βλέπει τα γεγονότα να συμβαίνουν στην ίδια θέση. Στην περίπτωσή μας, ο παρατηρητής στο Ο' μετράει τον ιδιοχρόνο. δηλαδή, ιδιοχρόνος είναι πάντοτε, ο χρόνος που μετρείται από έναν παρατηρητή ο οποίος κινείται μαζί με το ρολόι.
Είδαμε ότι τα κινούμενα ρολόγια «πάνε πιο αργά» κατά τον συντελεστή
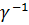 .
Αυτό ισχύει και για τα συνήθη μηχανικά ρολόγια, καθώς και για το ρολόι
«φωτός» που μόλις περιγράφηκε. Πράγματι, μπορούμε να γενικεύσουμε αυτά
τα αποτελέσματα αναφέροντας ότι όλες οι φυσικές διεργασίες,
συμπεριλαμβανομένων των χημικών αντιδράσεων και των βιολογικών
διεργασιών, επιβραδύνονται σε, σχέση με ένα ακίνητο ρολόι όταν
συμβαίνουν σε ένα κινούμενο σύστημα.
.
Αυτό ισχύει και για τα συνήθη μηχανικά ρολόγια, καθώς και για το ρολόι
«φωτός» που μόλις περιγράφηκε. Πράγματι, μπορούμε να γενικεύσουμε αυτά
τα αποτελέσματα αναφέροντας ότι όλες οι φυσικές διεργασίες,
συμπεριλαμβανομένων των χημικών αντιδράσεων και των βιολογικών
διεργασιών, επιβραδύνονται σε, σχέση με ένα ακίνητο ρολόι όταν
συμβαίνουν σε ένα κινούμενο σύστημα.Παραδείγματος χάριν, ο σφυγμός ενός αστροναύτη που κινείται στο Διάστημα θα πρέπει να προσαρμοστεί με την κλίμακα χρόνου ενός ρολογιού που βρίσκεται μέσα στο διαστημόπλοιο. Το ρολόι του αστροναύτη και ο σφυγμός του επιβραδύνονται σε σχέση με ένα ακίνητο ρολόι. Ο αστροναύτης όμως, προφανώς δεν αντιλαμβάνεται ότι ο ρυθμός ζωής επιβραδύνεται στο διαστημόπλοιο.
Η διαστολή του χρόνου είναι ένα πραγματικό φαινόμενο που έχει επιβεβαιωθεί με διάφορα πειράματα.
Αποσπάσματα από το βιβλίο: «Σύγχρονη Φυσική» - Κεφάλαιο 1ο των R.A.Serway – C.J.Moses – C.A.Moyer,
Πανεπιστημιακές Εκδόσεις Κρήτης 2001
Μέσα σε αυτό το νέο θεωρητικό πλαίσιο, ο χώρος και ο χρόνος παύουν
πλέον να είναι εκείνες οι απόλυτες και «άκαμπτες» δομές της κλασικής,
νευτώνειας φυσικής όπως αναφέρει στο ενδιαφέρον άρθρο του το Ευγενίδειο Ίδρυμα,
μέσα στις οποίες υλοποιούνται, ανεπηρέαστα απ’ αυτές, τα φυσικά
φαινόμενα, και η βαρύτητα παύει να είναι απλά αυτή η μυστηριώδης δύναμη
που έλκει ένα σώμα, δρώντας ακαριαία από απόσταση. Αντίθετα, μέσα από
μια σειρά πολύπλοκων και ιδιαίτερα δύσκολων στην επίλυσή τους εξισώσεων,
ο Αϊνστάιν θα περιγράψει τη βαρύτητα ως τη στρέβλωση που προκαλεί η
παρουσία της ύλης στη δομή του τετραδιάστατου χωροχρόνου.
Και ο χωροχρόνος, δυναμικός πλέον και όχι απόλυτος, καθορίζει με τη
σειρά του την τροχιά κάθε αντικειμένου, που κινείται εντός του, από
αυτόν ακριβώς τον βαθμό της καμπύλωσής του. Όπως το έθεσε αρκετά χρόνια
αργότερα ο φυσικός John Wheeler, «η ύλη υπαγορεύει στον χωροχρόνο πώς θα
καμπυλωθεί και ο βαθμός καμπύλωσης του χωροχρόνου υπαγορεύει στην ύλη
πώς θα κινηθεί».
Πολλές από τις θεμελιώδεις προβλέψεις της Γενικής Θεωρίας της
Σχετικότητας, από τη μετάπτωση του περιηλίου του Ερμή στην καμπύλωση του
φωτός και από την ύπαρξη των μαύρων τρυπών στη διαστολή του Σύμπαντος,
έχουν ήδη επιβεβαιωθεί. Ωστόσο, μία ακόμη από αυτές, στην οποία κατέληξε
ο ίδιος ο Αϊνστάιν ελάχιστους μήνες μετά τη δημοσίευση της Γενικής
Θεωρίας της Σχετικότητας, εξακολουθεί να αντιστέκεται στις προσπάθειες
των επιστημόνων να την επιβεβαιώσουν. Η πρόβλεψη αυτή δεν είναι άλλη από
την ύπαρξη των βαρυτικών κυμάτων.
Τα βαρυτικά κύματα είναι διαταραχές ή διακυμάνσεις στον ίδιο τον
ιστό του χωροχρόνου, οι οποίες διαδίδονται κατά τρόπο ανάλογο περίπου με
τους κυματισμούς που δημιουργούνται όταν πετάξουμε ένα βότσαλο μέσα σε
μια λίμνη. Σχεδόν κάθε μεταβολή στην κινητική κατάσταση ενός σώματος
(εκτός από την περίπτωση που η μεταβολή αυτή είναι σφαιρικά συμμετρική,
όπως κατά την σφαιρικά συμμετρική κατάρρευση ενός άστρου), αφήνει το
«αποτύπωμά» της στον χωροχρόνο με τη μορφή ενός βαρυτικού κύματος, το
οποίο απομακρύνεται από την «πηγή» του με την ταχύτητα του φωτός. Κάθε
βαρυτικό κύμα, κατά τη διάδοσή του, μεταβάλλει με συγκεκριμένο και
ρυθμικό τρόπο (επιμήκυνση σε μία διεύθυνση και συρρίκνωση κατά την
κάθετη διεύθυνση) τις αποστάσεις μεταξύ των ελεύθερων σωμάτων, σε ένα
επίπεδο κάθετο στη διεύθυνση διάδοσής του.
Προκειμένου να οπτικοποιήσουμε όσο είναι δυνατόν αυτές τις
ταλαντώσεις της ύλης που προκαλούνται από τα βαρυτικά κύματα, ας
υποθέσουμε αρχικά ότι παρατηρούμε από το πλάι ένα πλοίο που βρίσκεται
στη θάλασσα και ότι μία σειρά από κύματα το προσεγγίζουν επίσης από το
πλάι. Καθώς η κορυφή ενός θαλάσσιου κύματος διέρχεται κάτω από το πλοίο,
παρατηρούμε ότι το πλοίο «ανεβαίνει» σε ένα μέγιστο ύψος και στη
συνέχεια «κατεβαίνει», για να καταλήξει σε ένα ελάχιστο ύψος, όταν
ακριβώς από κάτω του βρίσκεται η «κοιλάδα» του κύματος κ.ο.κ.. Σε κάθε
περίπτωση, όμως, οι διαστάσεις του πλοίου παραμένουν αμετάβλητες.
Εάν, όμως, σε αυτό το «νοητικό» μας πείραμα αντικαθιστούσαμε τα
κύματα της θάλασσας με τα βαρυτικά κύματα, θα βλέπαμε κάτι εντελώς
διαφορετικό. Όταν, για παράδειγμα, η «κορυφή» του βαρυτικού κύματος
διερχόταν από το πλοίο, θα το «ξεχείλωνε», προκαλώντας διαστολή στο
μήκος του και ταυτόχρονη συρρίκνωση στο ύψος του. Στη συνέχεια, όταν η
«κοιλάδα» του βαρυτικού κύματος διερχόταν από το πλοίο, θα προκαλούσε
την αντίθετη μεταβολή, δηλαδή συρρίκνωση στο μήκος του και επιμήκυνση
στο ύψος του. Με δυο λόγια, εκείνες οι διαστάσεις του πλοίου, οι οποίες
είναι κατακόρυφες στη διεύθυνση διάδοσης του βαρυτικού κύματος, θα
μεταβάλλονταν περιοδικά.
Καθώς ένα βαρυτικό κύμα διαδίδεται στον χωροχρονικό ιστό του
Σύμπαντος, όσο περισσότερο απομακρύνεται από τη φυσική αιτία που το
δημιούργησε, τόσο περισσότερο εξασθενεί και τόσο περισσότερο
ελαχιστοποιούνται οι ταλαντώσεις που προκαλεί στην ύλη. Αυτή η
αλληλεπίδραση των βαρυτικών κυμάτων με την ύλη είναι μάλιστα τόσο
αμελητέα, που εάν κάποιο βαρυτικό κύμα, προερχόμενο από έναν γειτονικό
μας γαλαξία, διερχόταν από το Ηλιακό μας σύστημα, θα μετέβαλλε τη μέση
απόσταση της Γης από τον Ήλιο κατά απόσταση μικρότερη από τη διάμετρο
ενός ατόμου.
Το γεγονός αυτό αποδεικνύει και πόσο δύσκολο είναι να ανιχνευθούν
στην πράξη τα βαρυτικά κύματα. Χαρακτηριστικά παραδείγματα φαινομένων
που, όπως πιστεύουν οι επιστήμονες, είναι δυνατό να δημιουργήσουν
βαρυτικά κύματα ικανά να προκαλέσουν μετρήσιμες ταλαντώσεις στην ύλη,
αποτελούν και τα διπλά συστήματα άστρων νετρονίων, οι εκρήξεις
υπερκαινοφανών που δεν είναι σφαιρικά συμμετρικές, οι συγκρούσεις μεταξύ
αστέρων νετρονίων και οι συγχωνεύσεις γιγάντιων μαύρων τρυπών στους
γαλαξιακούς πυρήνες.
Παρόλο που τα βαρυτικά κύματα δεν έχουν ανιχνευθεί μέχρι σήμερα,
υπάρχουν ισχυρές ενδείξεις για την ύπαρξή τους. Η ισχυρότερη, ίσως, απ’
αυτές προέκυψε το 1974 με την ανακάλυψη ενός παράξενου αστρικού
συστήματος από τους Αμερικανούς αστροφυσικούς Russel Hulse και Joseph
Taylor, οι οποίοι για την ανακάλυψή τους αυτή τιμήθηκαν το 1993 με το
Νόμπελ Φυσικής. Με τη βοήθεια του γιγάντιου ραδιοτηλεσκοπίου Arecibo στο
Πόρτο Ρίκο, οι δύο επιστήμονες διαπίστωσαν ότι το σύστημα αυτό, 20.000
έτη φωτός μακριά από τη Γη, στον Αστερισμό Αετός, αποτελείται από έναν
πάλσαρ καθώς και από έναν ακόμη αστέρα, ο οποίος εικάζεται ότι είναι
αστέρας νετρονίων.
Οι αστέρες νετρονίων είναι τα αστρικά λείψανα, τα οποία
«επιβιώνουν» του εκρηκτικού διαμελισμού άστρων με μάζα πολλαπλάσια απ’
αυτήν του Ήλιου, κατά τη διάρκεια εκρήξεων σουπερνόβα. Οι πάλσαρ, από
την άλλη, είναι ταχύτατα περιστρεφόμενοι αστέρες νετρονίων με πανίσχυρο
μαγνητικό πεδίο, οι οποίοι εκπέμπουν από τους μαγνητικούς τους πόλους
στενές δέσμες ακτινοβολίας. Καθώς ένας πάλσαρ περιστρέφεται γύρω από τον
εαυτό του, οι δύο κώνοι ακτινοβολίας που εκπέμπει, «σαρώνουν» το
Διάστημα, ακριβώς όπως και το περιστρεφόμενο «μάτι» ενός φάρου.
Εάν η ακτινοβολία αυτή «τυχαίνει» να σαρώνει στο πέρασμά της τη Γη,
την αντιλαμβανόμαστε ως μια παλλόμενη πηγή ακτινοβολίας που
αναβοσβήνει, δηλαδή ως ένα παλλόμενο αστέρι (pulsating star, pulsar).
Ο πάλσαρ των Hulse-Taylor, όπως είναι σήμερα γνωστός, έδωσε στους
επιστήμονες ένα μοναδικό «εργαστήριο», με τη βοήθεια του οποίου
μπορούσαν να ελέγξουν συγκεκριμένες προβλέψεις της Γενικής Θεωρίας της
Σχετικότητας.
Η συστηματική του παρακολούθηση τα χρόνια που ακολούθησαν, οδήγησε
τους αστρονόμους στο συμπέρασμα ότι τα δύο αυτά ουράνια σώματα
περιστρέφονται με όλο και μεγαλύτερη ταχύτητα το ένα γύρω από το άλλο,
καθώς αργά αλλά σταθερά η μέση απόστασή τους μειώνεται, έτσι ώστε
υπολογίζεται ότι τελικά θα συγκρουστούν σε περίπου 300 εκατομμύρια
χρόνια. Γιατί όμως συμβαίνει αυτό; Σύμφωνα με τη Γενική Θεωρία της
Σχετικότητας, όταν ένα διπλό αστρικό σύστημα εκπέμπει βαρυτικά κύματα,
αποβάλλει ενέργεια, με αποτέλεσμα η τροχιά του να συρρικνώνεται και κατά
συνέπεια η περίοδός της να μειώνεται.
Οι μεταβολές αυτές, αν και ελάχιστες, έχουν ήδη μετρηθεί και
αντιστοιχούν με μεγάλη ακρίβεια στις τιμές που προβλέπει η Γενική Θεωρία
της Σχετικότητας, γεγονός που αποτελεί μια ισχυρή, αλλά παρόλ’ αυτά
έμμεση ένδειξη ότι τα βαρυτικά κύματα που προέβλεψε ο Αϊνστάιν όντως
υπάρχουν.
Πιο πρόσφατα, η ανακάλυψη του πρώτου διπλού πάλσαρ, του πρώτου
δηλαδή διπλού αστρικού συστήματος που αποτελείται από δύο πάλσαρ, έχει
δώσει την ευκαιρία στους αστρονόμους να ελέγξουν τις προβλέψεις της
Γενικής Θεωρίας της Σχετικότητας με περισσότερη ακρίβεια από ποτέ.
Αυτό το μοναδικό διπλό σύστημα πάλσαρ ανακαλύφθηκε το 2003
σε απόσταση μόλις 2.000 ετών φωτός μακριά, προς την κατεύθυνση του
Αστερισμού Πρύμνη. Σύμφωνα με τις έως τώρα παρατηρήσεις, η τροχιά του
συστήματος συρρικνώνεται κατά 7 χιλιοστά τον χρόνο, ακριβώς όπως
προβλέπει και η Γενική Θεωρία της Σχετικότητας
Εν ολίγοις αυτό που προσπαθούμε να δούμε είναι αν τα ταξίδια
του Enterprize στο θρυλικό Star Trek που ταξίδευε με ταχύτητες
πολλαπλάσιες του Φωτός καθώς ο "αντιδραστήρας αντιύλης του" μπορούσε να
καμπυλώσει τον Χωροχρόνο, είναι εφικτό να γίνουν.Η σκέψη είναι απλή, "δεν πάμε στο βουνό εμείς, φέρνουμε το βουνό σε εμάς", είναι η αντίστροφη πορεία του "αίτιου και αιτιατού" και αυτό από μόνο του, αρκεί για να αλλάξει τον τρόπο που σκέφτεται η Ανθρωπότητα.
Πηγή










